Who Is the Greatest Mathematician in the World?
Given its expansive and colourful history, the field of mathematics often sparks a number of discussions, including perhaps the most popular debate of all – who is the greatest mathematician in the world?
In this article, we’re looking into some of the biggest names in the field; if any of these individuals interest you, you might like to conduct your own research ahead of writing your personal statements and college applications.
The Global Impact of Mathematics
Since its conception, mathematics has played a key role in just about every scientific and technological field. These range from statistics and accounting to biotechnology and the recent innovations in artificial intelligence.
Beyond its interdisciplinary application, mathematical theories also underpin fields such as physics, engineering and cryptography. Take coding and coding software for example, which often rely upon mathematical formulas to draw conclusions.
Mathematicians also contribute to solving real-world challenges and societal issues, from the notable role of maths in World War II to its application in contemporary development of robotics in medicine.
If you’d like to explore the far-reaching impact of mathematics in more detail, our online Mathematics courses equip high school students with the relevant curriculum and experience to prepare for future careers in maths-related fields.
What Makes a Great Mathematician?
Before we can answer the question “who is the greatest mathematician in the world?”, it’s important to consider the complexity of the question.
Over the years, there have been leaders in the field across numerous historical periods, subfields and mathematical innovations, so identifying the greatest mathematician may be quite tricky. Greatness can be measured through ground-breaking discoveries in mathematics, the development of innovative theories, and lasting influence in the field.
The historical and cultural contexts surrounding each mathematician’s work also play a role in shaping perception of their greatness.
The Pioneers of Mathematics
Let’s start at the very beginning, with the notable ancient mathematicians who laid the foundation for mathematical thought and application in the generations to follow!

1. Pythagoras
Pythagoras was an ancient Ionian Greek philosopher and polymath, known for his teaching of metempsychosis – the idea that the soul enters a new body upon death.
Within the realm of geometry, Pythagoras is widely associated with his Pythagorean theorem, a product of Euclidean geometry that identifies the relationship between the three sides of a right triangle. This theory states that the square of the length of the hypotenuse (the longest side of a right-angled triangle) is equal to the sum of the squares of the lengths of the other two sides:
a² + b² = c²
Pythagoras also established the Pythagorean school of thought, which claimed that the universe and all things within it were made from numbers. From this, certain numbers were connected with certain ideas and concepts – in particular, the number three was attributed to the god Apollo, and believed to hold moral importance.

2. Euclid
Euclid, an ancient Greek geometer and logician, is widely considered the “father of geometry,” largely due to his ground-breaking work Elements. This treatise, understood to have been published in c. 300 BC, covers plane and solid Euclidean geometry, elementary number theory and incommensurable lines.
Elements offers the oldest deductive treatment of mathematics, establishing the foundations for geometry that remained widely unchanged until the 19th century.
Euclid is also known for creating a logical basis for his geometric theorems, understood as an axiomatic system – a set of hypotheses that can be used together to establish a given theorem. Axiomatic systems have remained an enduring part of geometric thought, with mathematicians continuing to use mathematical proofs in geometric theorising.

3. Archimedes
Archimedes, a Greek mathematician and contemporary of Euclid and Pythagoras, focused his work on levers, pulleys and the principle of buoyancy.
He is best known for inventing Archimedes’ principle, which states when an object is partially or fully immersed in a liquid, the apparent loss of weight is equal to the weight of the liquid displaced by it:
apparent weight = weight of object (in the air) – thrust force (buoyancy)
We can see the applications of Archimedes’ principle in the submarines and hot-air balloons of today!
Medieval Mathematicians
Following the pioneering theories of antiquity, the field of mathematics continued to evolve throughout the Middle Ages!
4. Al-Khwarizmi
Al-Khwarizmi was a Persian and Islamic mathematician who gained notoriety in the ninth century for his systematic solution of quadratic equations using the method we call “completing the square” today.
He uses the example equation below to complete the square:
x² + 10x = 39
In the below illustration, x² is represented by a square and 10x is represented by a rectangle, with the sum of these areas given to be 39. If we cut the rectangle into two parts, and attach these to adjacent sides of the square, the L-shaped can be filled with a smaller square to “complete” the larger square.
This increases the given area from 39 to 64, and the solution is as follows:
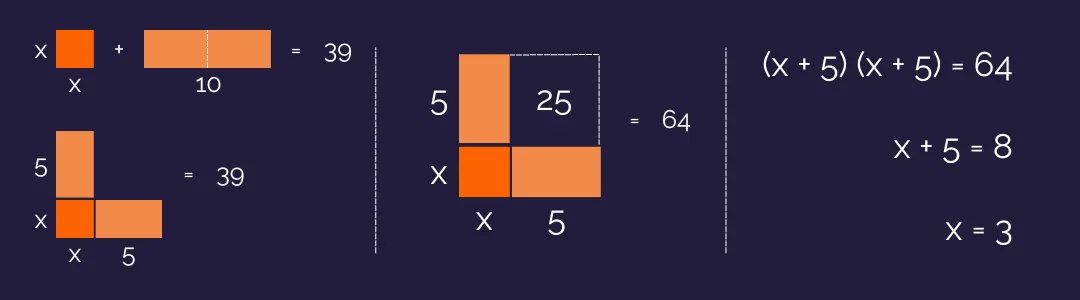
Additionally, Al-Khwarizmi achieved much of his greatness in his development of mathematical terminologies, including the terms algebra, algorithm and algorism. Given the role of these theories in mathematics, he’s widely hailed as the “father of algebra.”
Al-Khwarizmi’s key role in the invention of algorithms can be explored further through the modern-day study of Computer Science.
5. Omar Khayyam
Omar Khayyam was a Persian polymath, known for his contributions to mathematics, astronomy and philosophy. He contributed greatly to the field of algebra, using conic sections (curves produced by the intersection of a plane with a cone) to provide a complete classification of solutions to more than a dozen different forms of cubic equations!
Considered a precursor to Descartes, his work on geometric solutions and algebraic equations sought to unify the fields of algebra and geometry.
6. Leonardo of Pisa
Leonardo of Pisa, also known widely as Fibonacci, was an Italian mathematician considered to be “the most talented Western mathematician of the Middle Ages.” His work was influential in the establishment of the Hindu-Arabic numeral system in Europe, a system popularised via his 1202 composition, “Liber Abaci” (Book of the Abacus).
Fibonacci also introduced Europe and the Western world to much of Al-Khwarizmi’s work, as well as to the Fibonacci sequence – a sequence in which each number is the sum of the previous two numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…
Fibonacci used this sequence to calculate the growth of an idealised rabbit population over one year, however the sequence was first utilised in Indian mathematics as early as 200 BC by Pingala.
Revolutionary Thinkers and Innovators
Moving beyond the medieval period we come to the innovations that defined the Renaissance and Enlightenment eras in Europe.
7. René Descartes
Descartes was a French philosopher and mathematician, known for his groundbreaking exposition of analytic geometry. His work “La Géométrie” introduced today’s standard algebraic notation using lowercase a, b and c for known quantities, and x, y and z for unknown quantities.
He also invented the Cartesian Coordinate System, which describes the position of a two-dimensional point by a pair of numbers known as coordinates. These numbers signify the point’s horizontal (x) and vertical locations (y), so a series of points can be plotted on axes as a line or curve on a graph.
8. Leonhard Euler
Leonhard Euler was a Swiss mathematician and engineer, recognised for founding the studies of graph theory when he presented a solution to the Seven Bridges of Königsberg problem.
Euler also related the vertices (corners), edges and faces of a given polyhedron, discovering the formula:
V – E + F = 2
The constant in this formula is now known as the Euler characteristic for a planar graph, and ultimately led to the creation of topology – a branch of mathematics concerned with geometric configurations.
9. Pierre-Simon Laplace
Pierre-Simon Laplace was a French scholar and polymath, who contributed pioneering work in probability theory. He laid out a system of inductive reasoning based on probability, known today as Bayesian probability, or the process of using probability to predict the likelihood of future events.
Laplace also pioneered the Laplace transform, which has the form:
F(s) = ∫ f(t)e–st dt
This integral operator transforms a function of time (t) into a function of frequency (s), and has several applications in the study of Engineering today!
The Birth of Modern Mathematics
The birth of modern mathematics in the 17th and 18th centuries was fundamental in the development of abstract and formal mathematical theories.
10. Sophie Germain
Sophie Germain was a French mathematician, physicist and philosopher, who developed a pioneering theory of elasticity.
While her parents frowned upon her fascination with mathematics, given the assumed place of women in the 18th century, Germain continued to pursue mathematics by candlelight – eventually gaining the secret support of her mother!
With the 1794 opening of the École Polytechnique, Germain gained access to relevant lecture notes. After sending these notes to esteemed mathematician Joseph Louis Lagrange, she proved her aptitude as a scientist, and Lagrange took her on as a mentee in her own right.
For her work on elasticity theory, in which Germain derived a correct differential equation, she became the first woman to win a prize from the Paris Academy of Sciences.
Furthermore, she gained wide recognition for her substantial work on a general proof of Fermat’s Last Theorem in 1815. Whilst unpublished, Germain’s work proved the first case of Fermat’s Last Theorem for all odd primes p < 100.
11. Carl Friedrich Gauss
Carl Friedrich Gauss was a German mathematician and physicist, known predominantly for his contributions to algebra and number theory (the study of integers and arithmetic functions).
In particular, his 1797 doctoral thesis gave a proof of the fundamental theorem of algebra – that every polynomial equation with real or complex coefficients has as many roots as its degree.
In 1801, Gauss published a compilation of his mathematical findings, helping to consolidate number theory as a discipline. This work introduced the triple bar symbol (≡) for congruence, presented two proofs of the law of quadratic reciprocity, and developed the theories of binary and ternary quadratic forms.
Beyond number theory, he also made important contributions to differential geometry, studying curves and surfaces. Departing from the earlier work of Euclid and Descartes, Gauss measured the intrinsic curvature of a surface, from an inner point of view, rather than the way it’s embedded in space.
His work would prove crucial to the establishment of Non-Euclidean geometries – even coining the phrase himself! – allowing for later scientific discoveries like Einstein’s theory of relativity.
12. Augustin-Louis Cauchy
Augustin-Louis Cauchy was a French mathematician single-handedly responsible for the development of complex function theory, a branch of mathematical analysis that investigates functions of complex numbers.
His first proven theorem – now known as Cauchy’s integral theorem – was:
∫C f(z)dz = 0
Here f(z) is a holomorphic (complex-valued) function on and within the contour C lying in the complex plane. This finding still forms the core of complex function theory today.
Cauchy can also be remembered for his theory of elasticity, which describes the internal stress and strains in a solid body, resulting in crucial developments in the fields of continuum mechanics and the exploration of solid mechanics.
13. Georg Cantor
Georg Cantor was a German mathematician known for his groundbreaking work on set theory, where he provided a rigorous proof that there was more than one kind of infinity. To this point, in 1883, Cantor divided the infinite into the transfinite and the absolute.
Cantor’s theorem denotes that there are infinitely many infinite cardinal numbers, and that there is no largest cardinal number – the power set of a set A is strictly larger than the cardinality of A itself.
Cantor’s conception of transfinite numbers further enriched the concept of infinity as he developed an arithmetic of transfinite numbers that was similar to finite arithmetic.
20th Century Titans
The technological and social innovations of the 20th century were also accompanied by great mathematical developments…
14. Albert Einstein
Albert Einstein was a German-born theoretical physicist, best known for his contributions to quantum mechanics and his development of the theory of relativity. Widely considered one of the greatest scientists of all time, Einstein’s work was fundamental to the revolutionary reshaping of the nature of modern physics.
His mass-energy equivalence formula remains the world’s most famous equation, explaining how small amounts of mass (m) can be interchangeable with enormous amounts of energy (E):
E = mc²
Einstein’s revolutionary theory of relativity, published between 1905 and 1915, encompasses two interrelated physics theories: special relativity and general relativity. Special relativity explains how speed affects mass, time and space, while general relativity explains the law of gravitation.
The theory transformed theoretical physics, introducing concepts like kinematic and gravitational time dilation. Furthermore, his theory redefined the concepts of space, time, matter, energy and gravity.
15. John von Neumann
John von Neumann was a Hungarian-American mathematician, physicist and computer scientist, regarded as having perhaps the widest disciplinary coverage of his time.
Von Neumann played a pioneering role in the development of the modern computer, founding an architecture in which both data and program are stored in the same address space. This architecture is the basis of modern computer designs even today.
Von Neumann also played an instrumental role in the refinement of game theory. He was one of two scholars to construct a cooperative theory of n-person games, which assumed that various groups of players might join together to form coalitions.
If you’d like to learn more about modern computing, our online Computer Science course is taught by an expert tutor to help you get the edge for your future!
16. Kurt Gödel
Kurt Gödel was an influential mathematician and philosopher. Considered to be one of the most influential logicians in history, Gödel’s discoveries led to the proof of his incompleteness theorems.
These theorems were proven through a technique now known as Gödel numbering, in which a number is assigned to each symbol of a mathematical notation.
His first incompleteness theorem states that no consistent system of axioms, whose theorems can be listed by an algorithm, is capable of proving all truths about the arithmetic of natural numbers.
The second theorem, an extension of the first, shows that the system cannot demonstrate its own consistency.
Today, these theorems are widely interpreted as proof of the impossibility of finding a consistent set of axioms for all mathematics.
Contemporary Visionaries
While the idea of the “greatest mathematician” might inspire you to look to the history books for answers, there are several visionary mathematicians who continue to revolutionise the field today.
17. Andrew Wiles
Andrew Wiles is an English mathematician and a Royal Society Research Professor at the University of Oxford, specialising in number theory. He’s widely known for proving Fermat’s Last Theorem as a corollary of a limited form of the modularity theorem.
Wiles’ historic proof was based on his simultaneous proving of the modularity theorem, and was enough to imply the validity of Fermat’s Last Theorem. The proof has withstood ensuing mathematical scrutiny, and resulted in Wiles being named a recipient of the 2016 Abel Prize.
Wiles was also awarded a silver plaque from the International Mathematical Union (IMU) in 1998, which recognised his achievements.
18. Terence Tao
Terence Tao is an Australian mathematician and a professor of Mathematics at the University of California, Los Angeles (UCLA). His work specialises in the topics of harmonic analysis, algebraic combinatorics, number theory and partial differential equations.
Tao was a recipient of the Fields Medal in 2006, and his exceptional ability across a range of mathematical fields – co-authoring over 300 research papers – has earned him the distinction the “Mozart of mathematics”.
In particular, Tao has achieved great success in the field of number theory, proving the existence of arbitrarily long arithmetic progressions in prime numbers.
19. Maryam Mirzakhani
Maryam Mirzakhani was an Iranian mathematician and a professor of Mathematics at Stanford University, known for her distinguished work on the dynamics and geometry of Riemann surfaces and their moduli spaces.
She was the first woman and Iranian to be awarded the Fields Medal, a distinction she received in 2014. Mirzakhani’s ground-breaking work in hyperbolic geometry found that the rigidity of “homogenous space” is reflected in the dynamics of moduli space.
The Quest for the Greatest Mathematician
Our selections are only some of the notable scholars in the field of mathematics, and so the quest for the greatest mathematician in the world continues!
Most importantly, the legacy of these mathematicians collectively enriches human knowledge and understanding – and it’s this collective influence and greatness demonstrated by the above thinkers (and their contemporaries) that allows for a complex and storied set of mathematical traditions!

By Adam Kluge
Adam (he/him) recently completed his MSc in Criminology and Criminal Justice at the University of Oxford. His research exists at the intersection of law, politics, and history – and he welcomes opportunities to further explore these areas through personal and pedagogical practices. He completed his undergraduate degrees at Columbia University and will begin a PhD in Criminology at Oxford this autumn.
Delve deeper into Mathematics
Recommended articles
OxBright Tutors Share Their Top Tips for High School Graduates
Finishing high school can be a really intimidating juncture – you’re leaving the security of a routine you’ve followed for five plus years, and you’re faced with more options and less structure than ever before. Oh, and your decisions now can shape your future in a...
Which Career Is the Best Fit for Me?
Choosing your career path is one of the first big steps you’ll take as a young adult, so it can often be a daunting prospect. However, the possibilities are endless, and as long as you base your choices on your personal preferences, passions and interests, your...
How to Make a Study Schedule That Actually Works
Studying can sometimes feel like a daunting task, no matter how old you are or what level you’re studying at. You might be left thinking: How can I balance academics with my other commitments? How do I stay consistent with a study schedule? Is there a “good” or...



















